What is a Rogowski Coil?

Named after the German physicist Walter Rogowski, the Rogowski Coil is an electrical device used for measuring alternating current (AC) such as high speed transient; pulsed currents or power frequency sinusoidal currents.

In its simplest form a Rogowski coil is an evenly wound coil of N turns per metre on a non-magnetic former of constant cross sectional area A. The winding wire is returned to the starting point along the central axis of the former and the two ends are typically connected to a cable. The free end of the coil is normally inserted into a socket adjacent to the cable connection in a way that allows it to be unplugged thus enabling the coil to be looped around the conductor carrying the current to be measured.

How does it work?

An alternating or pulsed current in a conductor develops a magnetic field and the interaction of this magnetic field and the Rogowski coil local to the field gives rise to an induced voltage within the coil which is proportional to the rate of change of the current being measured. Provided the coil constitutes a closed loop with no discontinuities, it may be shown that the voltage E induced in the coil is proportional to the rate of change of the encircled current I according to the relationship E=H.dI/dt, where H, the coil sensitivity in (Vs/A), is proportional to NA.

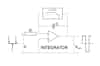
To obtain an output voltage V_OUT proportional to I it is necessary to integrate the coil voltage E; hence an electronic integrator is used to provide a bandwidth extending down to below 1Hz.

The op-amp integrator, in its simplest form, with an input resistor R_sh and feedback capacitor C has an output V_out=(1/CR)∫ Edt. The overall transducer gain is therefore given by, Vout=R_shI, where R_sh= H/CR is the transducer sensitivity (V/A).

The relationship V_out proportional to I is valid throughout the transducer bandwidth. The bandwidth is defined as the range of frequencies from f_L to f_H for which sinusoidal currents can be measured to within 3dB of the specified sensitivity R_sh.

At low frequencies the integrator gain increases and in theory will become infinite as the frequency approaches zero. This would result in unacceptable dc drift and low frequency noise; hence the integrator gain has to be limited at low frequencies. This limitation is achieved by placing a low pass filter in parallel with the integrating capacitor. The low pass filter sets the low frequency bandwidth f_L, typically this is less than 1Hz.

Furthermore, due to the distributed inductance and capacitance of the Rogowski coil there is a high frequency bandwidth f_H, (generally 1MHz or greater) above which the measurement is attenuated and significant phase delay occurs. The bandwidth of the electronic integrator and the length of cable connecting the integrator to the coil also influence this limit.

Over many years, PEM has developed  mathematical models of the Rogowski coil, cable and integrator allowing us to develop reliable, accurate current transducers in a variety of sizes for an ever growing market.

Using a Rogowski coil to measure AC or fast transient currents has many advantages over other methods of current measurement:

This page is intended to give you a brief overview of Rogowski Technology. If you would like to understand more about the technology please visit our publications page for access to our academic papers.

• Power Semiconductor Research & Development
• Small currents superimposed on large dc (e.g capacitor ripple)
• Fault Current Monitoring (over current detection)
• Energy monitoring (behaviour equivalent to class 0.5 current transformers)
• Lightning Strike Measurement
• Large ac currents (arc furnaces)
• High frequency sinusoids (e.g. induction heating, rf applications)
• Bearing and shaft currents in large machines
• Power measurement (accurate measurement of hf harmonics)

PEM offer a wide selection of Rogowski Current Transducers covering markets as diverse as power electronics development, industrial process control and protection & fault current monitoring. If you have any questions regarding the suitability of PEM Rogowski Transducers in your application please feel free to contact one of our engineers via the Contact page.